Content
- PageRank (lecture 4.1 & 4.2)
- Random walk and restarts (lecture 4.3)
- Matrix factorization and node embeddings (lecture 4.4)
1. PageRank
web page contains in-links and out-links
The importance of page can be defined as the number of in-links, AKA links as votes
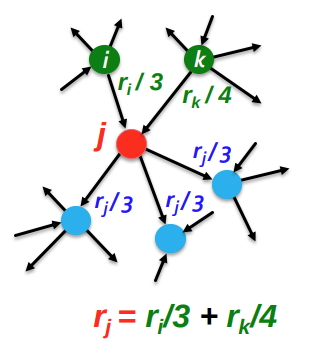
The flow model
Definitions:
- Rank $r_j = \sum_{i \rightarrow j} \frac{r_i}{d_i}$, where $d_i$ is out-defree of node i.
- Stochastic adjacency matrix $M_{ij} = \frac{1}{d_j}$, is a column stochastic matrix (columns sum to 1).
- Rank vector $r$, where $\sum_i r_i = 1$.
- $r = M r$.
Connect to random walk
Definitions:
- $p(t)$ probability distribution over pages
- $p(t+1) = M \dot p(t)$, $p(t)$ is a stationary distribution of a random walk.
solving eigenvector equation $\lambda x = A x$
Similarly, the rank vector $r$ can be seen as the eigenvector of $M$ with an eigenvalue of 1.